Idk why I put 'pretty happy' when I still might fail but I'm trying to stop that from happening.
ChatGPT has been saving my ass tbh. I should probably be using claude sonnet or smth (I heard that one's better at math) but it be working either way.
I had no idea this one was actually gonna be kinda fun. Like damn, I could've actually... like.... idk...
I wasn't really prepared :sob:
Like naw, I had no idea it was like programming. They literally be throwing loops at us and somehow it...... is the fibonacci sequence?????
I literally just have to get like 60% on the final and I'll pass the class. Like, damn.
But the most recent, final thing was so fun. Like, here's an example:
\( a_{n} = n^{2}-n \)
And you just have to write out the first 5 terms of the sequence.
So \( a_{1} = 1^{2}-1 \)
\( a_{2} = 2^{2}-2 \)
\( a_{3} = 3^{2}-3 \)
\( a_{4} = 4^{2}-4 \)
\( a_{5} = 5^{2}-5 \)
\( = 0 \)
\( = 2 \)
\( = 6 \)
\( = 12 \)
\( = 20 \)
Pretty easy, right!?!?!? I wasn't expecting it to be fun.
Heres more, since I need better notes anyways:
Simply decide whether this sequence is finite or infinite.
\( a_{1} = 8; \text{for } n \ge 2, a_{n} = 2(a_{n-1}) \)
It kinda looks confusing if you've never seen it but it's pretty easy if you recognize it.
(plus tell me how this isn't literally programming)
Well, it's kinda the same thing.
\( a_{1} \) is 8, and from there on, the previous one is doubled!
So of course, it is infinite.
--------------
Alr this next one is fun.
Find the first 6 terms of this sequence:
\( a_{1} = 7, a_{2} = 7; \text{for } n \ge 3, a_{n} = a_{n-1} + a_{n-2} \)
Again, looks complicated but it's not.
\( a_{1} = 7 \)
\( a_{2} = 7 \)
(We know that just from the question)
\( \text{for } n \ge 3 \) meaning the following ones:
\( a_{3} = a_{2} + a_{1} \)
\( a_{4} = a_{3} + a_{2} \)
\( a_{5} = a_{4} + a_{3} \)
\( a_{6} = a_{5} + a_{4} \)
(7 + 7 = 14)
(14 + 7 = 21)
(21 + 14 = 35)
(35 + 21 = 56)
So the sequence goes (7, 7, 14, 21, 35, 56)
This is literally fibonacci sequence. SO COOL.
--------------
Now we learn about summation notation! It's this weird thing: \( \sum_{}^{} \)
It basically just means get the sum of these things (add them all together).
For example:
\( \sum_{k=1}^{4}2^{k} \)
Though its sometimes written this way, here's what it should usually look like:
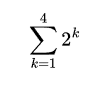
This just means start at the bottom number (k = 1), keep going until the top number (4), and each term you do the thing on the side (\( 2^{k} \)).
\( k = 1: 2^{1} = 2\)
\( k = 2: 2^{2} = 4\)
\( k = 3: 2^{3} = 8\)
\( k = 4: 2^{4} = 16\)
Then we just add these all up!
The answer here is 30!
--------------
alr, next, we have write the series using summation notation:
\( 1 + \frac{1}{2^{2}} + \frac{1}{3^{2}} + \frac{1}{4^{2}} + \frac{1}{5^{2}} \)
The answer here is:
\( \sum_{k=1}^{5}\frac{1}{k^{2}} \)
Because
\( k = 1: \frac{1}{1^{2}}\) (which is just 1)
\( k = 2: \frac{1}{2^{2}}\)
\( k = 3: \frac{1}{3^{2}}\)
\( k = 4: \frac{1}{4^{2}}\)
\( k = 5: \frac{1}{5^{2}}\)